Overview

For the first part of this project, I explored diffusion models to generate, restore, and transform images by iteratively denoising them from pure noise to realistic visuals. Using the DeepFloyd IF model, I implemented tasks like inpainting, hybrid imagery, and visual anagrams.

Intial Sampling of Model

I sampled using 'a man wearing a hat' and played around with the number of interference step. I found that while smaller steps were much quicker the quality was much less realistic. While larger steps took longer, but looked much more realistic.

an oil painting of a snowy mountain

a man wearing a hat

a rocket ship

10 steps

20 steps

100 steps

Sampling Loops

In this task, I implemented the forward diffusion process to add controlled Gaussian noise to a clean image at specific timesteps, simulating how images degrade over time. Using this noisy data, I explored two denoising approaches: classical Gaussian blur filtering and a pretrained UNet model. The Gaussian blur provided a basic but limited ability to reduce noise, while the UNet, leveraging its pretrained knowledge, reconstructed the original image more effectively by estimating and removing the added noise. I visualized the results for each timestep to compare the original, noisy, and reconstructed images, highlighting the power of diffusion models in reversing noise for high-quality restoration.

Timestep 250

Noisy

Guassian Denoised

Predicted Image

Timestep 500

Noisy

Guassian Denoised

Predicted Image

Timestep 750

Noisy

Guassian Denoised

Predicted Image

Iterative Denoising

This code implements an iterative denoising process to reconstruct a clean image from a noisy one using a diffusion model. Starting with a noisy image at a specified timestep, the iterative_denoise function progressively reduces noise step by step, leveraging the pretrained UNet model to estimate the clean image (x0_estimate) and compute the predicted image for the next (less noisy) timestep. The process follows equations from Denoising Diffusion Probabilistic Models (DDPM), iteratively refining the image until it approaches the original clean version. To enhance realism, variance is added at each step using the add_variance function. The function also visualizes the denoising progress at regular intervals, showcasing the gradual reduction of noise.

Noisy Campanile at t=690

Noisy Campanile at t=510

Noisy Campanile at t=330

Noisy Campanile at t=150

Original

Iteratively Denoised

One Step Denoised

Guassian Denoised

Diffusion Model Sampling

I started with random noise and used a diffusion model guided by the prompt "a high quality photo" to generate five unique images. By iteratively denoising each sample, I gradually transformed the noise into coherent, realistic visuals aligned with the given prompt.

Sample 1

Sample 2

Sample 3

Sample 4

Sample 5

Clasifier Free Guidance

In this implementation, I used Classifier-Free Guidance (CFG) to generate images from random noise, leveraging both conditional and unconditional prompt embeddings. Unlike the earlier iterative_denoise function, which solely relies on the conditional prompt for denoising, CFG combines conditional and unconditional noise estimates to guide the model more strongly toward the desired prompt ("a high quality photo"). The guidance is achieved by amplifying the difference between the conditional and unconditional estimates using a scale factor, improving the alignment of the generated images to the text prompt. This approach enhances the quality and specificity of the generated images while maintaining diversity, resulting in more coherent and visually appealing outputs compared to standard iterative denoising.

Sample 1

Sample 2

Sample 3

Sample 4

Sample 5

Image-to-image Translation

I apply noise to the input image at different levels, based on specified start indices, to create progressively noisier versions. For each noisy image, I use Classifier-Free Guidance (CFG) to iteratively denoise it, aligning the output with the prompt "a high quality photo." This process generates unique edits of the original image, depending on the amount of initial noise I introduce. I then compare these edits with the original image to observe how varying noise levels influence the final results.

Original

Index 1

Index 3

Index 5

Index 7

Index 10

Index 20

Original

Index 1

Index 3

Index 5

Index 7

Index 10

Index 20

Original

Index 1

Index 3

Index 5

Index 7

Index 10

Index 20

Editing Hand-Drawn and Web Images

In this step I use previous CFG model to generate an image taken from the web and two hand drawn images.

Original

Index 1

Index 3

Index 5

Index 7

Index 10

Index 20

Original

Index 1

Index 3

Index 5

Index 7

Index 10

Index 20

Original

Index 1

Index 3

Index 5

Index 7

Index 10

Index 20

Inpainting

Now, I implement an inpainting function that uses diffusion models to reconstruct parts of an image based on a binary mask. During each denoising step, I preserve the original content where the mask value is 0 and allow the model to generate new content where the mask value is 1, ensuring seamless blending. This approach effectively edits specific regions of an image while maintaining the original structure and detail in unedited areas.

Original

Mask

Replacement

Inpainted

Original

Mask

Replacement

Inpainted

Original

Mask

Replacement

Inpainted

Text-Conditioned Image-to-image Translation

I add noise to the original image at different levels and use CFG to iteratively denoise it, guided by the text prompt "a rocket ship." The process generates multiple variations of the image, where higher noise levels lead to more significant changes aligned with the rocket ship prompt. By displaying the original image alongside these variations, I demonstrate how the diffusion model transforms the image differently based on the initial noise level while adhering to the provided prompt.

Original

Index 1

Index 3

Index 5

Index 7

Index 10

Index 20

Visual Anagrams

In this part, I am creating a visual anagram where it appears as one image from one orietation and another the otherway. At each timestep of the denoising process, I calculated noise estimates for both prompts—one for the normal orientation and one for the flipped image—and combined them with a weighted average, giving slightly more emphasis to the "old man" prompt for balance. I repeat the process for the others.

Old Man

Campfire

Dog

Oil Painting of Snowy Village

Rocket

Oil Painting of Man

Hybrid Images - A collection of Skulls

I implemented a function to create hybrid images by blending two distinct concepts—"a lithograph of a skull" and "a lithograph of waterfalls." At each timestep of the denoising process, I generated noise estimates for both prompts and applied a low-pass filter to the first prompt (skull) to emphasize its broader features, while applying a high-pass filter to the second prompt (waterfalls) to preserve its finer details. By combining these filtered frequencies, I constructed an image that visually shifts between the two concepts, depending on the viewing distance or focus. I tested different random seeds to fine tune.

Skull & Waterfall

Skull & Campfire

Skull & Snowy Oil Painting

In this section of the project, we aim to train a U-Net model to denoise noisy MNIST digits. To prepare the training dataset, we first introduce noise to the MNIST images. Below are examples showcasing different noise levels:

Using a sigma=0.5 level, I trained the UNet model so it can learn to denoise noisy digits into sharper images of the number.

This is an example result after 1 epoch.

This is an example result after 5 epochs.

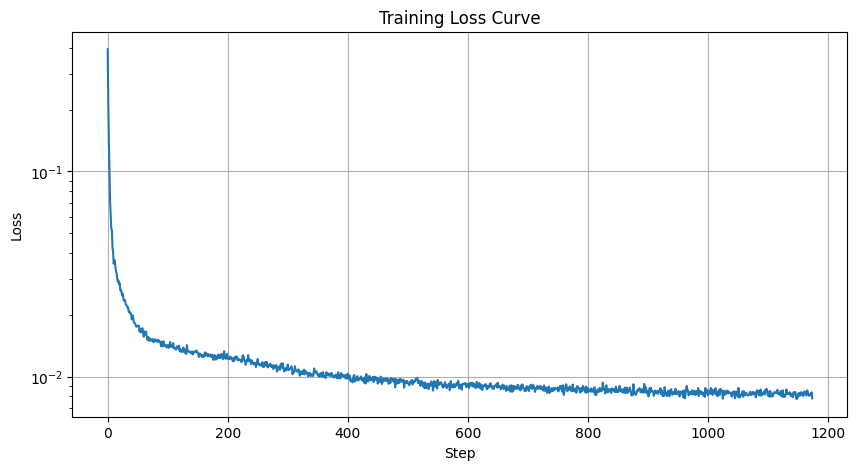
While running the model I recorded the loss after every iteration and this is the resulting graph:

Finally, while running the model I recorded the results at various noise levels:

Part 2

In this part, I modified my U-Net so it predicts the noise in an image instead of directly denoising it. This change is based on what I learned in Part A: iterative denoising works much better than trying to denoise everything in one step. I also added timestep conditioning to the U-Net, so the model knows exactly which step of the diffusion process it’s working on. This helps it adapt its predictions to the specific amount of noise present at each stage.

To train the model, I took random batches of images, added noise to each image using a random timestep (from 0 to 299), and passed the noisy images through the U-Net. A timestep of 0 means no noise at all, while 299 means the image is pure noise. The model then predicted the noise that was added, and I calculated the loss by comparing the predicted noise to the actual noise that was applied. This way, the U-Net learns to understand how to work with all levels of noise in the diffusion process.

For sampling, I followed the iterative denoising process I used in Part A. I started with an image made entirely of noise and ran it through the U-Net multiple times, step by step, reducing the noise in stages. Since the model was trained on all kinds of noise levels, it could handle the denoising process effectively and recover a clean image by the end of the iterations. Here are some of the results I got from my time-conditioned U-Net, showing how it transforms pure noise into recognizable images:

After Epoch 5

After Epoch 20

Here is my MSE Loss Graph:

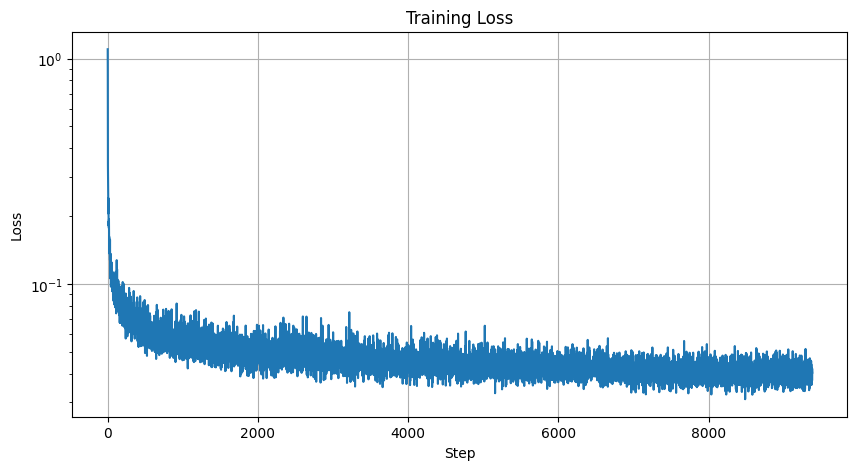
Loss Graph

Now, I will enhance the UNet by incorporating class conditioning. This modification allows the model to utilize class-specific information during training, enabling it to denoise images more effectively. By training the UNet on specific digit images along with their corresponding labels, the model learns to better reconstruct and generate images of numbers. This also gives me the ability to generate images of specific digits by conditioning the UNet on the desired class. This approach is similar to providing a text prompt to a generative model and obtaining an image aligned with the prompt. In this case, instead of text prompts, I use class labels (e.g., digits 0–9) to guide the image generation process. Below, I present the results demonstrating the improvement achieved by adding class conditioning to the UNet.

After Epoch 5

After Epoch 20

Here is my MSE Loss Graph:

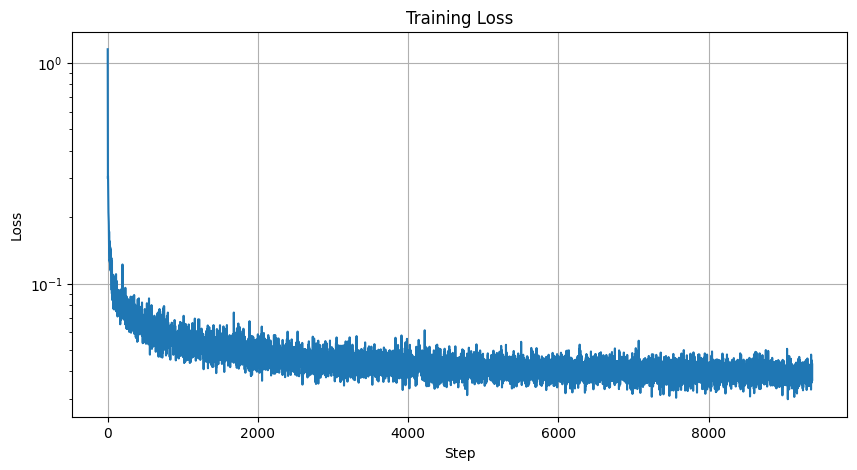
Loss Graph