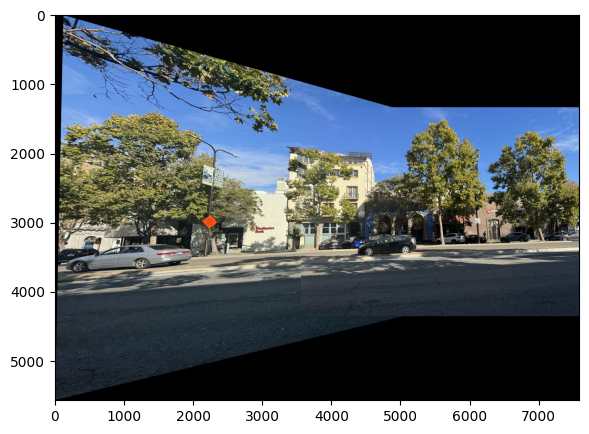
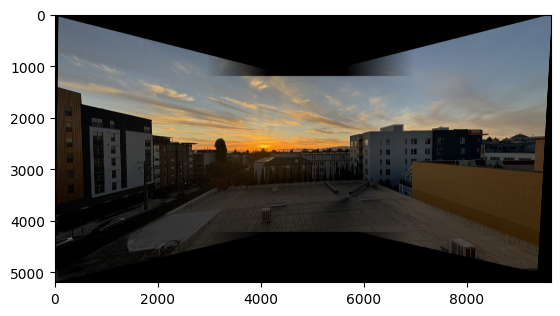
Shoot the Pictures
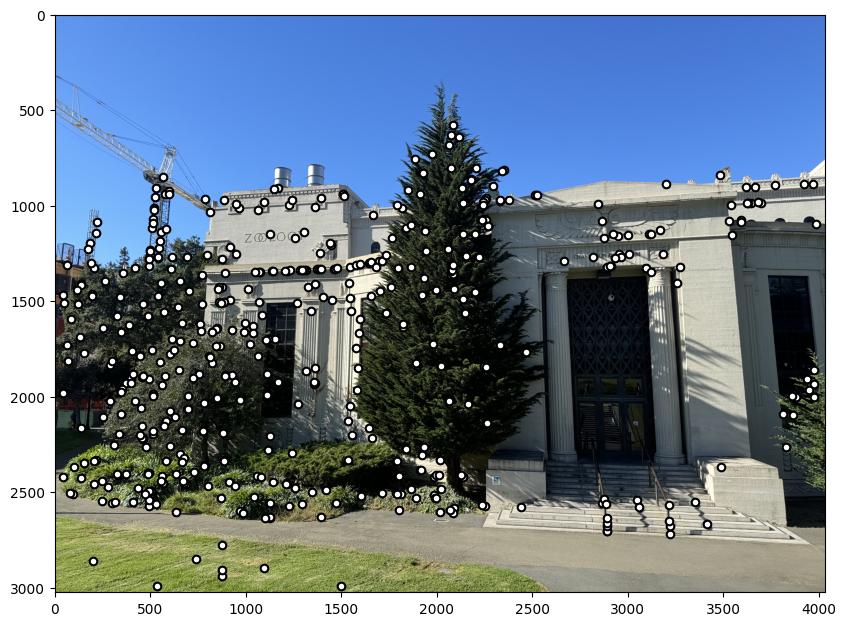
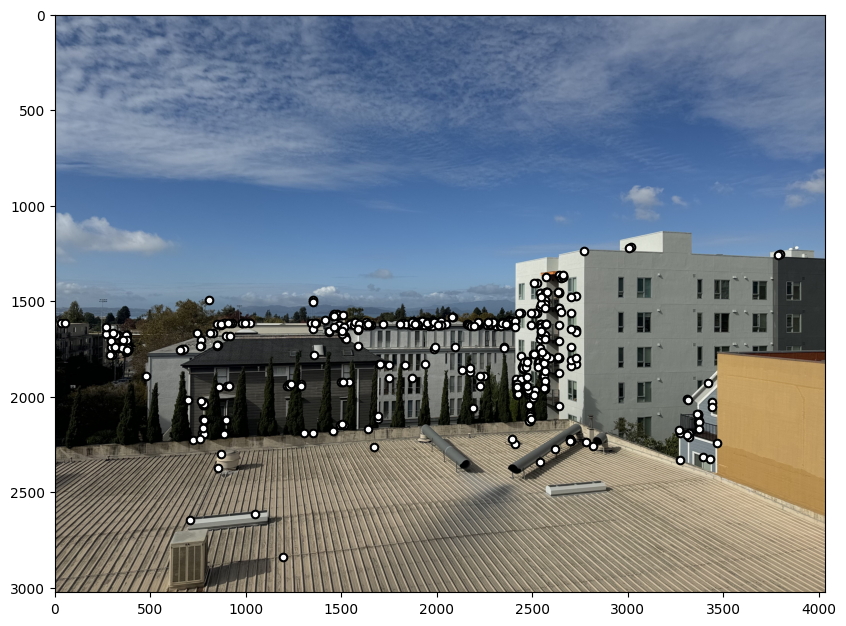
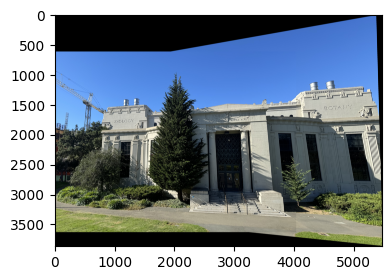
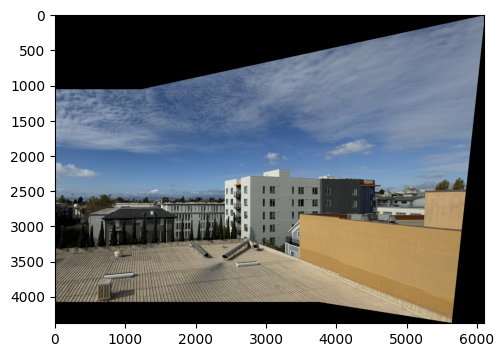
To begin I shot some pictures with large overlap such that I can stitch together to create a larger image later on in the project. Below are some examples:








For the first part of this project, I will be creating a homogrophy function and a warping function for the purpose of rectifying an image and creating a mosaic or a stictching a multiple images. For the second part, I developed an automated correspondence detection tool to enable mosaic creation without manual point selection. I implemented Adaptive Non-Maximal Suppression, Feature Descriptor extraction and matching, and RANSAC, following the methods outlined in the paper "Multi-Image Matching using Multi-Scale Oriented Patches" by Brown et al.








The homography matrix, \( H \), is a 3x3 matrix that maps points from one plane to another through a projective transformation. Given a set of corresponding points in two images, the goal is to find the matrix \( H \) that transforms a point \( (x, y) \) from the first image to a point \( (x', y') \) in the second image. The transformation can be written as:
\[ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = H \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]
The homography matrix \( H \) has 8 unknowns, as the last element is set to 1 for the scaling of the image. The matrix is of the form:
\[ H = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & 1 \end{bmatrix} \]
For each pair of corresponding points \( (x, y) \) in the first image and \( (x', y') \) in the second image, we can derive two linear equations by rearranging the transformation:
\[ x' = \frac{h_{11}x + h_{12}y + h_{13}}{h_{31}x + h_{32}y + 1}, \quad y' = \frac{h_{21}x + h_{22}y + h_{23}}{h_{31}x + h_{32}y + 1} \]
Multiplying both sides by the denominators to eliminate the fractions, we get:
\[ x'(h_{31}x + h_{32}y + 1) = h_{11}x + h_{12}y + h_{13} \] \[ y'(h_{31}x + h_{32}y + 1) = h_{21}x + h_{22}y + h_{23} \]
Rearranging terms, we obtain a system of linear equations of the form \( A h = b \), where \( h \) is the vector of unknowns:
\[ A = \begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -x'x & -x'y \\ 0 & 0 & 0 & x & y & 1 & -y'x & -y'y \end{bmatrix} \]
\[ b = \begin{bmatrix} x' \\ y' \end{bmatrix} \]
By stacking these equations for all corresponding points, we can solve the linear system using least squares to estimate the homography matrix \( H \).