Project 3: Face Morphing

Overview

In this project, I am creating a morph animation by combining both shape warping and color blending between two images. The process has two main components: color blending, or cross-dissolving, and shape warping. While blending colors is relatively simple, the real challenge lies in accurately warping the shape of one image to match the other. To achieve smooth transformations, I define correspondences between key facial features, such as aligning the eyes, mouth, chin, and ears in both images. This careful mapping ensures that the transition looks natural and fluid, producing a seamless morph effect.

Part 1: Defining Correspondences

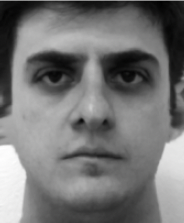
To morph two faces, we begin by identifying corresponding points on each face. We then use triangulation based the corresponding points to map out the face. Specifically, we apply Delaunay triangulation to the average of the two point sets. For my example, I used my face and professional basketball player Stephen Curry. Below I show the selected points, Delaunay triangles, and the average of the two Delaunay triangles.

My Keypoints

Curry's Keypoints

Delaunay Triangles on Me

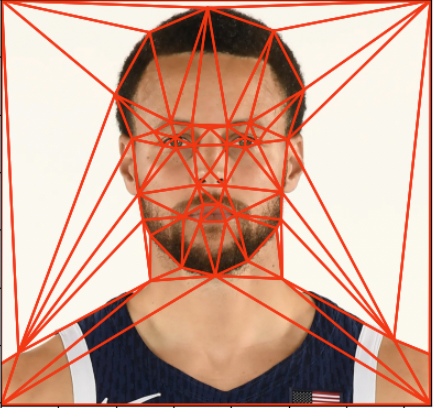
Delaunay Triangles on Curry

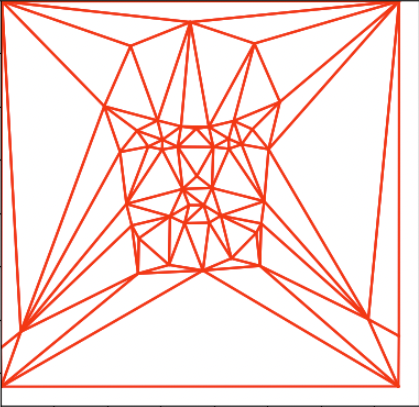
Average Delaunay Triangles

Part 2: Computing the "Mid-way Face"

To create a mid-way face between two different faces, the first step is to compute the average shape by finding the mean of each corresponding point between the two faces. This average set of points then serves as the basis for Delaunay triangulation. Next, both faces are warped to match this average shape. This involves using an affine transformation matrix to adjust each triangle in the triangulation so that it aligns with the corresponding triangle in the average shape. Finally, the colors of the warped faces are blended together. For the warping process, I used skimage.draw.polygon to generate a triangular mask from the vertices, allowing for efficient warping of all points within each triangle simultaneously. I use bilinear interpolation to provide color accuracy of each of the triangles. The result is a blended image where you can see the features of each person.

Aadit

Mid-way Face

Curry

Part 3: The Morph Sequence

To create the morph sequence, I used a similar method as part 2, however using fractions I manipulated how much each image is portrayed in a morph. When a parameter was 0, I was the full image, however when the fraction was 1 the full image was Steph Curry. For each of the 45 frames a different weightage of each image is seen producing the morph sequence below. One key optimization I made was using nearest neighbor to optimize the function rather than using interpolation. Esentially rather than interpolating everytime we use the color of the nearest neighbor to speed up the process.

Morph Sequence

Part 4: The "Mean face" of a population

In this part I used the FEI Face database, which has 200 images from both male and females containing them smiling and a nuetral face. For this phase, I only used the nuetral faces. This database came with precropped images as well as 46 keypoints for each image. I added an additional 4 points on the corners to better help with mapping along the edges. To find the average shape I found the mean of all the keypoints and then I warped each face into the set of keypoints I found and used cross-disolving to get the average colororation. Below is the average face I obtained:

Average Face

Below are 3 examples of sample points warped to the average face. I demonstrated a variety of race and gender for the examples:

Original 1a

Morphed 1a with Average Face

Original 10a

Morphed 10a with Average Face

Original 12a

Morphed 12a with Average Face

Below is an image of my face warped to the average person. I believe the reason my ear is appeared blurred is because there were no keypoints in the sample dataset outlining an ear and as you can see in the average face the ears are not seen. I also have the average face morphed onto my face below. I did this by mapping a one to one correspondance to each of the keypoints using Delaunay triangles as before and then warping in the same process as before.

My Face to Average Face

Average Face to My Face

Part 5: Caricatures - Extrapolating from the mean

By leveraging the population averages from the FEI database, we can create caricatures through extrapolation. I approached this by treating the correspondences on my neutral face as a vector p and those on the average expression face as a vector q. I then calculated new target correspondences using the formula p+1.5(q−p), found the extrapolated triangulation, and warped my face to align with these exaggerated target points. You can see from the images how negative numbers squish my face, while positive numbers >1 widen my face. By paying close attention to features like the mouth and nose you can distinctly see this difference.

Original Image

Caricature alpha=-0.9

Caricature alpha=-0.5

Caricature alpha=1.1

Bells and Whistles

For my Bells and Whistles I decided to change both my gender and ethnicity of my face. I did this by first morphing my face onto a chinese woman. I then morphed the coloration using cross-disolve. I then put the two together to obtain the final result.

My Face

Average Chinese Woman

Shape Morph

Appearence Morph

Full Morph